Hiperism Consulting, LLC: HCTR-2004-1

COMPARING COMPILERS ON INTEL™ PENTIUM 3 and PENTIUM 4 PROCESSORS WITH THE KALLMAN INTEGER AND LOGICAL ALGORITHM

George Delic

HiPERiSM Consulting, LLC.

This is part of a series of reports on a project to evaluate industry standard fortran 90/95 compilers for IA-32 Linux™ commodity platforms. This report shows results, in a side-by-side comparison for each compiler, for the Intel™ Pentium 3 (P3) and Pentium 4 Xeon (P4) processors for the Kallman algorithm.

Results for the wall clock time are compared for two benchmarks compiled using three different Fortran compilers with the Linux™ operating system and one with Windows 2000. For this project benchmarks were executed in serial mode on a dual processor Intel™ Pentium III (256KB L2 cache) and a dual processor Pentium 4 Xeon 3.06GHz (1MB L3 cache). These architectures offers Streaming Single-Instruction-Multiple-Data Extensions (with version 2, SSE2, for the Xeon). This enables vectorization of loops operating on multiple elements in a data set with a single operation. Since SSE/SSE2 instructions are irrelevant for non-floating point operations they are not implemented in this report.

The choice of compilers for Linux™ IA-32 platforms now includes several vendor-supported products. The importance of this category is that vendor products have technical support and undergo continuous development with ports to new architectures as they arrive in the marketplace. The four compilers chosen in this survey are described separately in the following sections and compiler switches used in the benchmark are also discussed.

Absoft f77 and f90/f95 are the Fortran compilers included in the Absoft Pro Fortran™ 8.0 package for Linux™ offered by the Absoft Corporation (http://www.absoft.com). The f90/f95 version has a Cray front-end and resulted from a five-year collaboration with Cray Research. With this compiler use of the –O3 compiler switch enables automatic architecture detection and selection of the Pentium 3 or 4 instruction set.

The Intel Fortran Compiler version 8.0 targets both Intel IA-32 and IA-64 (Itanium) architectures, but only the former has been used in this project so far. Details on the compiler features are available at HiPERiSM Consulting, LLC’s URL. Code for target architectures is generated with either the switch –tpp6 (v 7.1 on the Pentium 3) or –tpp7 (v8.0 on the Pentium 4).

The Lahey/Fujitsu Fortran 95 compiler (hereafter Lahey) for Linux™ is available from Lahey Computer Systems, Inc., (http://www.lahey.com). The Express version 5.6 for Microsoft Windows 2000™ was used on the P3 because it was available from another project for the same hardware. With this compiler use of the –tpp switch to enable automatic architecture detection for the P3 only. However, release v7.1 (for Windows) and v6.2 (for Linux) support a --tp4 compiler switch to target the Pentium 4 Xeon. The v6.2 release and the new switch is used here for the P4 Xeon processor.

The pgf90™ fortran compiler (Linux™ distribution) from the Portland Group, (http://www.pgroup.com) was used in the CDK 4.0 release where it supports OpenMP, MPI and OpenMP+MPI parallel applications on HiPERiSM’s IA-32 Linux™ cluster. With this compiler use of the –fast compiler switch enables automatic architecture detection. Note that the CDK 5.1 release (not used here) may offer additional performance enhancement of the Pentium 4 Xeon processor.

Portability issues come up when legacy Fortran code needs to be compiled. In this respect a compiler that allows extensions to the f90/f95 standard can save time and effort. The two compilers that offer the widest scope in portability are those from Absoft and Portland. Compilers from Lahey and Intel are less forgiving of such extensions. For example the Kallman algorithm used logical operators such as the IAND, IOR, and NOT intrinsic functions that are now part of the Fortran 90 standard and require integer operands. The older FORTRAN 77 standard .AND., .OR., .NOT. for integer operands no longer applies under Fortran 90 because these operators are reserved for logical operands. Nevertheless, different compilers apply different extensions to the standard and two of the compilers discussed below (Absoft and Portland) compile the older FORTRAN 77 standard (with the default Fortran 90 options) without comment. The Lahey compiler does not allow the extensions and reports compiler errors if they are used.

Here we also mention some migration issues that came up with compiler and architecture changes. The change in architecture from P3 to P4 Xeon also involves changes in library versions. As a result, two of the compilers had to either be upgraded or have patches applied. Installation of the Absoft 8.0 compiler for the Xeon processor and the newer Linux Kernel does require download and application of two patch files to resolve glibc version issues (these patch files are available from the Absoft URL given in Section 3.1). Likewise, an attempt was made to install the 7.1 release of the Intel Fortran compiler on the P4 Xeon. However, again version skew with glibc suggested the simpler option of installing the 8.0 release. For similar reasons, the Lahey 6.2 release was not installed on the Pentium 3. Whenever the version of a compiler is changed performance is also expected to change. This is especially true of the Intel compiler since major performance improvements are announced with the 8.0 release. Therefore, the changes in performance reported here for the Intel compiler are due to improvements in the compiler technology as well as the change in architecture.

The algorithm used here has been executed on a wide variety of platforms and is an excellent benchmark in studying how a compiler and architecture interact for the types of operation they use. A fuller discussion of the benchmarks is available in previous reports (HCTR-1999-1, HCTR-2001-1). What follows is only a brief introduction.

The Kallman algorithm computes the permanent of a (0,1) matrix with high efficiency using only integer and logical operations and some of the MIL-STD-1753 bit intrinsic functions that are now part of Fortran 90/95. There is no floating point work in the Kallman algorithm. A fuller discussion of results is given by Delic and Cash (2000). This algorithm is CPU intensive and performs a small amount of I/O only at the beginning and end of each run. Memory access requirements are negligible and because of the small instruction set, the instruction buffer fetch rates are amongst the smallest we have seen. On the IA-32 platform the executing code requires of the order of 1MB of memory so that on the Xeon processor it is expected to test the limits of processor-cache bandwidth and latency. This algorithm runs in scalar mode because of a complex branching structure that inhibits vectorization. Six cases where used in this analysis corresponding to data sets with matrix sizes N=30, 44, 48, 52, 56, 60.

The following sections summarize execution time with four compilers for the Kallman algorithm for six data sets (or Cases).

Whole code execution was measured with the Linux™ time command. This choice was due in part to the problem of portable timing procedures in the different compilers. Wall clock time was also measured with a Fortran 90/95 SECNDS routine and differences from the time command introduced an error of approximately 2% and was therefore deemed to be of sufficient accuracy for these simple benchmarks. Note that this particular fortran routine is not portable, and may produce different results with different compilers (e.g. the Portland compiler only reports the time to the nearest second).

For the Kallman algorithm the choice of compiler switches for the Xeon processor is summarized in Table 5.1. For the Pentium III case the only differences are the use of the Intel 7.1 and Lahey 5.6 releases. Timing results are shown in Tables 5.2 (Pentium 3) and 5.3 (Pentium 4). Figures 1 and 2, for Pentium 3 and Pentium 4 respectively, show the ratio of these times to the compiler that reports the smallest execution time for the six cases.

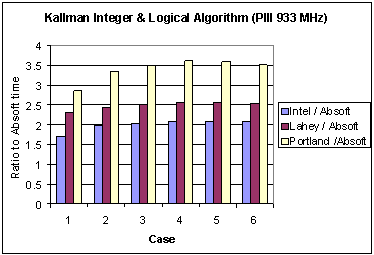
Fig. 1 Ratio of execution times of three different compilers to that for the Absoft compiler with the Kallman algorithm on the Pentium 3.

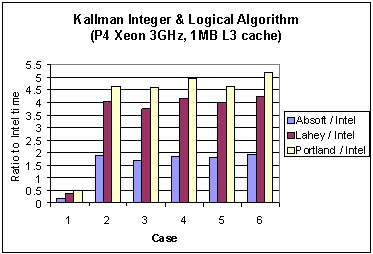
Fig. 2 Ratio of execution times of three different compilers to that for the Intel compiler with the Kallman algorithm on the Pentium 4 Xeon.

It is interesting to observe the changes in performance between the Pentium 3 and 4. On the Pentium 3 the Absoft compiler reported the lowest wall clock times, whereas on the Pentium 4 the Intel compiler does so. To compare the performance gain for each compiler due to a change in architecture Figure 3 shows the ratio of the Pentium 3 execution times to those of the Pentium 4. Except for Case 1, the performance gain is of the order of 8 or better. It is surmised that this is due to effective cooperative use of processor and cache by the Intel compiler. A deeper performance analysis of the underlying reasons for these results is the subject of a future report.

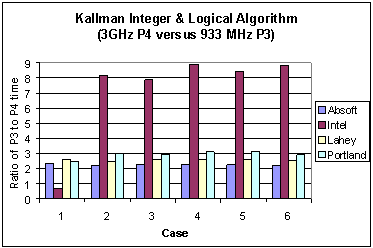
Fig. 3 Ratio of execution times of four different compilers on the Pentium 3 versus the Pentium 4 Xeon for the Kallman algorithm.

It is instructive to compare theses results with those for the Pentium II in the first of these reports (HCTR-1999-1) for the Absoft compiler on the Pentium II processors. The P4 Xeon results reported here take 18-20 times less execution time. This improvement is due to performance developments in both compiler and architecture technologies.

This report presented performance results of four fortran compilers in the IA-32 environment. The variability in performance found was specific to the benchmarks selected and represented extremes in arithmetic operation types. For the Kallman algorithm performance results were excellent in the transition from P3 to P4 and corresponding compiler versions. Variability in performance results is expected between compilers and the details showed these to be large. This was due to the exceptional performance of the Intel 8.0 compiler. From this result it may be surmised that with the P4 Xeon architecture, when codes require little to no memory traffic, performance results may be very good.

The analysis in subsequent reports will include in-depth evaluation of performance of this group of compilers with specialized software such as the Intel VTune™ Performance Analyzer. Also in this evaluation the consequences of compiler switches for numerical precision and stability will be investigated.

Delic, G.and Cash, G., 2000: The Permanent of 0,1 Matrices and Kallman's Algorithm, Comput. Phys. Comm., 124, 315-329.