Hiperism Consulting, LLC: HCTR-2010-5

1.0 EXPLORING CMAQ ON A GPGPU

1.1 Thread-safe version of CMAQ

HiPERiSM's thread parallel version of the CMAQ Rosenbrock solver (ROS3-HC) is used as the starting point to explore a port of CMAQ to a General Purpose Graphical Processing Units (GPGPU) device. The host CPU architecture for this exploration was a platform with dual Intel™ quadcore (X5450) CPUs and one Nvidia™ GPGPU (C1060) device in a PCIe x16 slot. While this is not state-of-the-art at this time, it is sufficient to establish feasibility and identification of the issues involved in porting CMAQ to a GPGPU device. For more details on this configuration see Table 2.1 of Technical report HCTR2010-1. The following discussion refers to two user selectable parameters, BLKSIZE and NCMAX. These parameters are fully described in a previous report in this series (HCTR2009-1). They were included in the design of ROS3-HC to enable selection of chunk size (BLKSIZE) for OpenMP threads and vector length (NCMAX) for SSE enabled loops in CMAQ's ROS3-HC thread parallel solver.

1.2 Porting CMAQ to a GPGPU

A successful port of CMAQ ROS3-HC to a GPGPU device requires either multilayered loop nests, or very long (single) loops to reap the benefits of the many threads such devices employ. This suggests that if the NCMAX “vector” length could be made very large there could be throughput benefits for a CMAQ parallel version adapted for such devices. If at the same time, the number (BLKSIZE) of cells in a block could be increased, then the number of such blocks passed to the solver would be reduced. Consequently, the number of calls to the CMAQ chemistry solver algorithm is fewer, and loops spanning the entire block would be off-loaded to the many-core device.

1.3 Benchmark of CMAQ loop nests

In these benchmarks the vector length for loops over domain cells was set equal to the block size (NCMAX= BLKSIZE) with values of BLKSIZE incremented in a wide range. Table 1.1 shows the vector length increments chosen for this analysis on both the host CPU (X5450) and the GPGPU device (C1060). The domain size of 2,276,640 cells corresponds to the episodes described in Section 3 in the report HCTR-2010-1.

Table 1.1. Domain size and choices for vector length.

Range of vector lengths used in benchmarks for the host CPU and GPGPU device
Domain size (279x240x34)	Blocksize (vector length)	Number of blocks (calls to the solver)
2276640	256	8894
2276640	512	4447
2276640	1024	2224
2276640	2048	1112
2276640	4096	556
2276640	8192	278
2276640	16384	139
2276640	32768	70

For timing benchmarks several loop nests from the CMAQ ROS3-HC thread parallel version were selected. Table 1.2 lists the legend for the loop names and details of each source code construct are described in the next section. These are not the only types of loops encountered in the ROS3-HC solver, but they are a starting point for identifying porting issues and GPGPU versus CPU performance results.

Table 1.2. Loop names for loop nest benchmarks.

CMAQ-ROS3 solver loops used in benchmarks
Loop name	Number of loop nests in parallel region	Loop nest depth
L478	1	2
L522-37	2	2
L1240	2	2 and 1
L1284	3	1, 2, and 1

2.0 COMPILING THE LOOP NESTS

The Portland 10.6 Fortran compiler was used with the pgf3 compiler group. For the host CPU the loops were compiled as single threaded loops. In the GPGPU case, the Portland Accelerator™ compiler generated kernels and data movement for the target device by recognition of accelerator directives (!ACC) that encapsulated loop nests in the benchmarks. In conducting these benchmarks no additional GPGPU optimizations were performed.

3.0 CODE FOR LOOP NESTS

3.1 Loop L478

! Line 478

!$ACC REGION

DO NRX = 1, NUSERAT( NCSP ) ! sequential

NRK = NKUSERAT( NRX, NCSP )

DO NCIN = 1, NUMCELLS ! parallel

RXRAT( NCIN, NRK ) = RKI( NCIN, NRK )

ENDDO

!$ACC END REGION

Loop L478 is one example of a construct that recurs in CMAQ's Rosenbrock solver: the outer loop has an indirect memory reference to extract the index NRK that is used in the inner loop. Therefore the outer loop cannot be parallelized. The inner loop over the index NCIN is a parallel candidate over the vector length NUMCELLS (=NCMAX).

3.2 Loop L522-37

! L522-37

DO 111 NRX = 1, NUSERAT( NCSP )

NRK = NKUSERAT( NRX, NCSP )

ISP3 = NREACT( NRK )

c..Calculate reaction rate

IF( ISP3 .GT. 0 ) THEN

DO NR = 1, ISP3 ! sequential

ISP1 = IRM2( NRK, NR, NCS )

DO NCIN = 1, NUMCELLS ! parallel

RXRAT( NCIN, NRK ) = RXRAT( NCIN, NRK ) *

& Z ( NCIN, ISP1 )

ENDDO

ENDIF

c..Subtract loss terms from dc/dt for this reaction

!$ACC REGION

DO NR = 1, ISP3 ! sequential

ISP1 = IRM2( NRK, NR, NCS )

DO NCIN = 1, NUMCELLS ! parallel

ZDOT( NCIN, ISP1 ) = ZDOT( NCIN, ISP1 ) -

& RXRAT( NCIN, NRK )

ENDDO

c..Add production terms to dc/dt for this reaction

DO NP = 1, NPRDCT( NRK ) ! sequential

ISP1 = IRM2( NRK, NP + 3, NCS )

XTEMP = SC( NRK, NP )

DO NCIN = 1, NUMCELLS ! parallel

ZDOT(NCIN, ISP1 ) = ZDOT( NCIN, ISP1 ) +

& XTEMP * RXRAT( NCIN, NRK )

ENDDO

!$ACC END REGION

111 CONTINUE ! END LOOP OVER REACTIONS

Loop L522-37 is another example of a construct that recurs in CMAQ's Rosenbrock solver:the DO 111 loop has an indirect memory reference to extract the index NRK that is used in contained loop nests. There are three contained loop nests and each has an outer loop that again has an indirect reference used in the inner (long) vector loop. These inner vector loops are all candidates for parallel execution while the outer loops execute sequentially.

3.3 Loop L1240

! Line 1240

!$ACC REGION

DO N = 1, N_SPEC ! parallel

DO NCIN = 1, NUMCELLS ! parallel

YP( N, NCIN ) = Z(NCIN, N ) + B1 * K1(NCIN, N ) +

& B2 * K2(NCIN, N ) + B3 * K3(NCIN, N )

K4( N, NCIN ) = ( D1*K1(NCIN, N ) +

& D2*K2(NCIN, N ) + D3*K3(NCIN, N ) )

ENDDO

DO NCIN = 1, NUMCELLS ! parallel

Y( NCIN , N ) = Z(NCIN, N )

ENDDO

!$ACC END REGION

Loop L1240 computes the final solution of the Rosenrock iteration. It differs from the previous examples in two respects: the loop nest has depth 2, and the first inner loop has significant arithmetic operation count (5 adds and 6 multiplies) which bodes well for a GPGPU kernel. The second inner loop is a memory copy which may be a performance deficit. Note that reversing loop order in the first loop pair would invoke non-unit stride for multiple arrays on the right hand side. All loops in L1240 are candidates for parallel execution.

3.4 Loop L1284

! Line 1284

!$ACC REGION

ERR = 0.0D+00 ! parallel

DO NCELL = 1, NUMCELLS ! parallel

DO N = 1, N_SPEC ! sequential

YTOL = ATOL( N ) + RTOL( N ) * ABS( YP( N, NCELL ) )

ERR( NCELL ) = ERR( NCELL ) + ( K4( N, NCELL ) / YTOL ) ** 2

ENDDO

MAXERR = 0.0D0

DO NCELL = 1, NUMCELLS ! parallel

MAXERR = MAX( MAXERR, UROUND, SQRT( ERR( NCELL ) * RNSPEC ) )

ENDDO

!$ACC END REGION

For the current Rosenbrock iterate, Loop L1284 computes the mean square error (MSE), ERR, for each cell index, NCELL, as a sum over a chemical species index N. This creates a loop carried dependence on ERR that prevents parallel execution of the species loop with index N. The last loop is a reduction loop searching for the maximum of the root MSE. The three loops that are candidates for parallel execution are as indicated.

4.0 RUNTIME RESULTS

For the ROS3-HC version of CMAQ timing benchmarks were performed for each loop nest described above. Results for execution on both the host CPU and the GPGPU device are presented in the previous report (HCTR2010-4). The most promising results are for the L1240 case because it is also the most computationally intensive case.

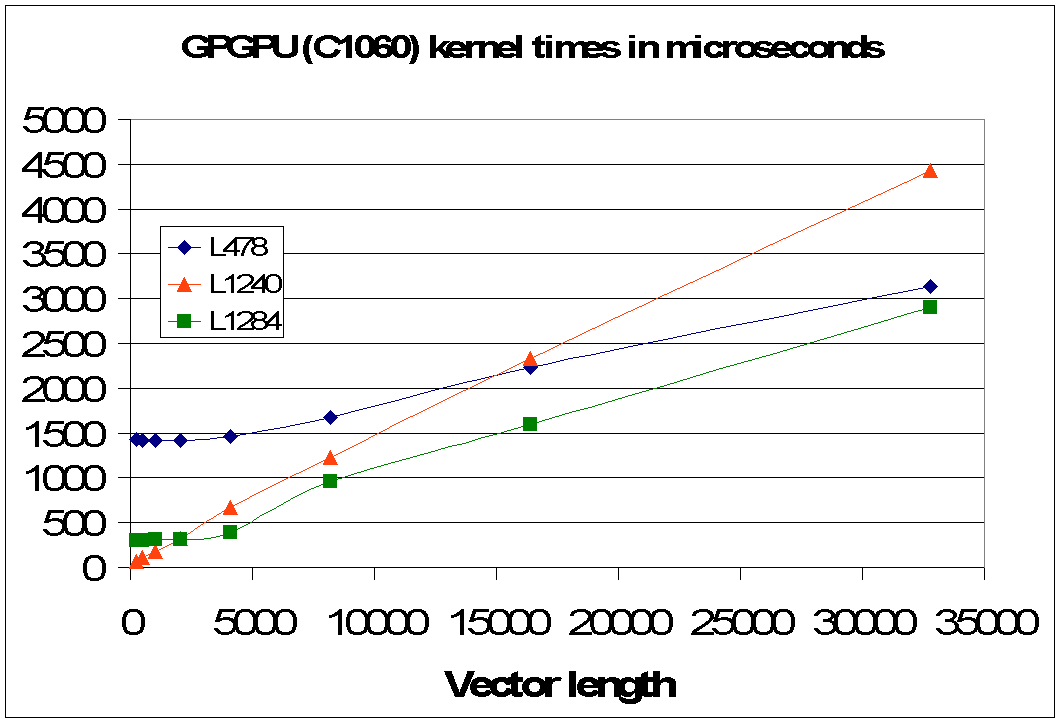
Fig 4.1: Scaling of time spent in kernels on the GPGPU device versus the vector length for three CMAQ benchmarks in Table 1.2.

5.0 CONCLUSIONS

Exploratory benchmarks with selected loops on a many-core GPGPU device suggest that opportunities exist for CMAQ on such devices, but further work is needed to improve performance.